Wow danke, das nenne ich mal ne Hammer Antwort und hilft sogar einen Mathe-Schwächling wie mir
Irgendwie hatte ich auch mal etwas ähnliches im Kopf, aber Mathematisch hätte ich das wohl nicht lösen können.
Also ich habe alles verstanden mit dem Koordinatensystem dessen Achsen auf der Linie des Dreiecks liegen, jedoch bin ich ein wenig mit der Gleichung überfordert, hoffe du nimmst es mir nicht übel
Sehe ich das so richtig, das die Gleichung angibt (und falls das eine richtig dumme Frage ist, sag es mir bitte damit ich mich später vergraben kann
) das x,y aus a+ub_1+vb_2 berechnet werden kann und u,v aus a + (b_1 b_2)?
Das ist eine Gleichung, die zweite Zeile ist lediglich eine Termumformung um aus den zwei getrennten Gleichungen eine zu machen. Die Gleichung ließ sich "so herum" einfach aufstellen. Aber von den Größen x, y, a, u, b1, v, b2 hast du ja alle bis auf u und v. Daher musst du die Gleichung noch umstellen, damit du u und v ausrechnen kannst
Und dieses Umstellen kannst du hier mit einer Matrixinversion lösen. Aber damit es eine Matrix zum invertieren gibt, musst du die Vektoren vorher in eine Matrix schreiben. Immer dran denken, Matrizen sind nicht so irre kompliziert Konstrukte - sie dienen in erster Näherung dazu, dass man bei vielen Gleichungen, die zusammen hängen, nichts verwechselt. Man könnte das ganze auch durch "scharfes hingucken" oder probieren lösen.
Zitat:
Wegen @Namenloser (Danke an der stelle
) weiss ich ja das die eingeklammerten Basisvektoren Blockmatrizen sind, jedoch habe ich leider noch nie mit Matrizen gearbeitet und bisher immer versucht diese zu umgehen da es mir auf den ersten Blick zu kompliziert aussah, jedoch können sie sehr nützlich sein in dem Gebiet
Kann ich bestätigen, sind sehr nützlich
Zitat:
deshalb würde ich gerne den Umgang mit ihnen lernen. Wäre die Matrix so korrekt?:
Code:
[b_1_1, b_2_1
b_1_2, b_2_2]
Ja, genau das habe ich hier auf dem Zettel stehen
Zitat:
Oder was ich mir auch überlegt habe ist, ob ich irgendwie die Basisvektoren und u und v in eine Matrix schreiben soll, da es ja nebeneinander, aber das wäre ja auch komisch weil ich u und v ja noch gar nicht habe?
u und v sind nur Skalare, die kannst du untereinander in einen Vektor schreiben. Man
kann Skalare als 1x1 Matrizen und Vektoren als 1xn Matrizen sehen, aber für mich fangen
richtige Matrizen™ bei 2x2 an.
Umgestellt sieht die Gleichung so aus:
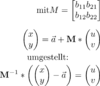
Und damit kannst du jetzt u und v ausrechnen. Beachte, dass das inverse wirklich links stehen muss, die Multiplikation ist nicht vertauschbar. Die Matrixinversion kannst du analytisch machen, die Formel dazu
gibt es bei Wikipedia.
Zitat:
Wie du siehst bestehen bei mir noch einige Unklarheiten, jedoch glaube ich das wenn ich das mit der Blockmatrix begriffen habe, sollte ich die Formeln auch hinbekommen.
Delphi bietet ja in der
Unit 
System.Math.Vectors eine schöne
TMatrix Struktur. Diese wollte ich nun für einige Berechnungen zum testen benutzen, jedoch ist diese Standardmässig irgendwie nur eine 3x3 Matrix oder sehe ich das falsch? Wenn ich ja die restlichen "Felder" auf 0 setze klappt das ja nicht mehr wie es soll. Wäre es sinnvoller dafür ein eigenes Konstrukt zu bauen oder geht das auch irgendwie mit der Hauseigenen Lösung?
Was die konkrete Implementierung angeht, kann ich dir leider nicht so viel helfen, da ich schon lange nicht mehr Delphi gemacht habe. Aber die Mathematik sollte hier wie da funktionieren. Und es müsste eigentlich auch mit 3x3 Matrizen gehen, wenn du rechts und unten 0 hinschreibst.