Ja klar

(Ziel war es auch, auszuloten was genau ich noch weiter erklären muss

)
Also alles etwas ausführlicher: Du hast ein 3D-Dreieck mit den Punkten A, B und C. Diese hast du in eine Ebene projiziert, nennen wir die Punkte a, b und c. (klein)
Ausgehend von dem Punkt a kannst du nun ein neues, angepasstes Koordinatensystem definieren. a ist der Ursprung, die Strecke
ab die eine Achse und
ac die andere. Das ist dann nicht rechtwinklig, aber es funktioniert trotzdem. Vorteil ist, dass du alle Punkte im Dreieck als Vielfache der beiden Strecken angeben kannst.
Für einen beliebigen Punkt im 2D-Dreieck (x, y) brauchst du nun die Koordinaten in dem neuen Koordinatensystem. Nennen wir die Variablen (u, v) dann ergibt sich folgendes:
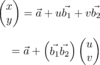
Mit den "Basisvektoren" b_1 und b_2. B_1 = b-a und b_2 = c-a. Die kannst du einfach nebeneinander in eine 2x2 Matrix schreiben.
Das ist jetzt ein lineares Gleichungssystem (kurz LGS) das sich gut lösen lassen sollte. (Wenn du nicht weist wie, frag nochmal nach. Wenn die Determinante der Matrix 0 ist, ist dein Dreieck nicht wohldefiniert.)
Wenn du das LGS gelöst hast, kannst du eine Formal für u und v hinschreiben. Diese überträgst du dann in das Programm und bekommst dann für jeden beliebigen Punkt die Werte u und v.
Anschließend rechnest du folgendes:
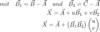
Das Ergebnis (der Vektor X) ist dein Punkt im 3D-Raum.