|
 |
 |
 |
 |
|
|
|
|
(Co-Admin)
Registriert seit: 30. Mai 2002 Ort: Hamburg 13.920 Beiträge Delphi 10.4 Sydney |
#1
Hallöle,
im Rahmen meines Studiums hatte ich mich mal mit diversen Suchfunktionen beschäftigt. Suchen kann man viel - insbesondere wenn der Tag lang ist - aber ich suche Knoten in einem Graphen. Das klingt sehr theoretisch, ich werde aber gleich Beispiele liefern, die das Thema greifbarer machen werden. Stellen wir uns vor, wir hätten ein Labyrinth. Schön mit Mauern drin sowie jeweils einem Start- und einem Zielpunkt. Aufgabe der Suchfunktion ist es jetzt, einen gültigen Weg vom Start zum Ziel zu finden. Gültig ist so ein Weg dann, wenn (a) das Spielfeld nicht verlassen wird und (b) keine der unüberwindbaren Mauern überschritten wird. Aber oftmals wollen wir ja nicht nur irgendeinen Weg haben, sondern vielleicht einen Weg, der bestimmte Eigenschaften erfüllt: Zum Beispiel den kürzesten Weg - oder den Günstigsten. Oder wir setzen noch früher an und wollen erstmal wissen, ob es überhaupt irgendeinen Weg gibt - mit welchen Eigenschaften auch immer dieser versehen sein mag. Ihr seht, es gibt also verschiedene Fragestellungen und seid vermutlich wenig überrascht, wenn ich hier unterschiedliche Lösungsansätze präsentiere. Und so unterschiedlich die Lösungen auch sind, so wenig unterscheidet sich ihre Implementierung. Genau genommen tauschen wir immer nur einen Funktionsaufruf aus und erhalten das jeweils gewünschte Ergebnis. Mehr dazu gleich. Zuerst möchte ich Euch die Grundlagen umreißen und Euch eine Vorstellung der verschiedenen Verfahren geben. Danach sehen wir uns an, wie man so etwas implementieren ("proggen" oder "c0den" für die Jüngeren unter uns) könnte. Ich werde im Folgenden die Landschaft skizzieren, in der wir uns bewegen. Für dieses Tutorial nutze ich bewusst eine einfache Landschaft. Das Konzept, das dahinter liegt, lässt sich je nach eigenem Wunsch auch auf deutlich komplexere Sachverhalte anwenden. Als Randbedingung gilt hier grundsätzlich: Die Labyrinthe müssen endlich sein. Kommt man in den Bereich der unendlichen Mengen rein, wird's noch mal eine Ecke komplizierter. Denken wir an ein rechteckiges Labyrinth, welches mit Spielfeldern versehen ist. Ein gültiger Zug geht stets in eine der vier Himmelsrichtungen. Eine diagonale Bewegung ist der Einfachheit halber nicht vorgesehen, das Beispiel kann jedoch leicht um weitere Bewegungsrichtungen erweitert werden. Das Labyrinth könnte also wie folgt aussehen: Schwarz die Felder, die unüberwindbar sind, rot der Startpunkt und grün der Zielpunkt:  Fangen wir an und lassen den Rechner feststellen, ob es überhaupt einen Weg gibt, der vom Start zum Ziel führt. Sicherlich - wir sehen das auf einen Blick, aber der Rechner "weiß" das gegenwärtig noch nicht. Optimal wäre ein Verfahren, das sofort den "besten" Weg liefert. Mal abgesehen davon, dass wir noch nicht definiert haben, was der beste Weg tatsächlich ist, kann ich Euch gleich enttäuschen: So ein Verfahren gibt es nicht für allgemeine Problemstellungen. Das ist eines der uralten Desaster der Menschheit: Geschwindigkeit vs. Qualität - im Allgemeinen kann man nur eines davon haben. Ich sage: Na und? Spielt doch keine Rolle. Einen rechenintensiven Algorithmus, der uns dann den besten Weg liefert, können wir immer noch ransetzen, wenn wir erstmal wissen, ob es überhaupt einen Weg gibt - also ob sich der Aufwand tatsächlich lohnt. Und hier kommt die Tiefensuche ins Spiel. Sie kann sehr schnell eine klare Aussage treffen, ob es einen Weg gibt. Und sie liefert uns im Erfolgsfall sogar einen Weg - der jedoch meist mehr einer Stadtrundfahrt im Labyrinth ähnelt als einem Weg, den wir wirklich haben wollten. Aber das ist egal. Die Aussage "ja, es gibt einen Weg" ist für uns von Bedeutung. Die Tiefensuche Die Tiefensuche gehört zu den sog. uninformierten Such-Verfahren. Sie schnappt sich den ersten Knoten und schaut von dort aus, in welche Richtungen sie sich weiterbewegen kann. Wenn also nicht gerade eine Mauer im Weg ist oder der Rand des Labyrinths, so kann sich sie in unserem Szenario nacheinander auf alle vier Nachbarfelder bewegen. Anschaulich formuliert steht sie auf ihrem Feld und guckt in die Runde. Alle gültigen Nachbarfelder werden dabei gleich behandelt und wenn sie noch nicht betreten wurden, so kommen sie in eine TODO-Liste -der Container- und zwar in der Reihenfolge, in der sie betrachtet wurden. Nachdem die Nachbarfelder beäugt wurden, greift die Tiefensuche in den Container und zupft sich das oberste Element heraus. "oben" ... "unten" - das hört sich verdächtig nach einem Stack an. Ist auch einer. Der Container wird also als Stack benutzt. Dieses herausgegriffene Element wird nun als Ausgangspunkt genutzt und die Suche beginnt von vorn - genau so lange, bis der Container leer ist, weil es keine weiteren Nachbarfelder mehr gibt oder das Ziel gefunden wurde. Der geradezu bombige Vorteil dieses Verfahrens liegt darin, dass es im Vergleich zu anderen Verfahren sehr schnell ist. Aber - bitte beachten - die gefundene Lösung ist fast immer nicht die optimale Lösung. Sehen wir uns ein Beispiel an, in dem die Tiefensuche beendet wurde. Die blauen Felder liefern einen möglichen gültigen Weg vom Start zum Ziel. Die Wegstrecke habe ich durch Pfeile markiert:  Also schön - es gibt einen Weg. Immerhin. Aber diese schnörkelige Strecke können wir nicht brauchen. Jetzt kommen wir also zu dem Punkt, an dem uns der gefundene Weg interessiert. Nehmen wir an, wir wollten einen möglichst kurzen Weg haben. Dann wäre es doch legitim, so lange in Richtung des Zieles zu marschieren, bis wir an eine Wand stoßen. So ähnlich geht das Hillclimbing-Verfahren vor. Die Hillclimbing-Suche (Bergsteiger-Algorithmus) Hier kommen wir zu den ersten "informierten" Suchverfahren. Es werden nämlich nicht wie bei der Tiefensuche alle Nachbarfelder als gleichwertig betrachtet, sondern vorrangig die Felder, die uns näher zum Ziel bringen. Es werden also wieder alle begehbaren Nachbarfelder betrachtet. Diese werden dann sortiert in den Container gelegt. Die Sortierung erfolgt auf Basis der Entfernung vom Ziel. Felder, die einen näher bringen, sind erstmal "besser" als Felder, die dies nicht tun - Kriterium ist also die verbleibende Wegstrecke zum Ziel. Es werden trotzdem alle begehbaren Nachbarfelder, also auch die "weniger guten", in den Container gelegt - man weiß ja nie... Dumm nur, wenn wir dabei in eine Sackgasse laufen. Sackgassen? Ja, aber klar doch. Folgendes Bild als Beispiel (rot = Start, grün = Ziel, schwarz = Mauer):  Auf den ersten Metern fühlt sich dieser Algorithmus als der Gewinner schlechthin. Immerhin ist er auf direktem Wege zum Ziel. Aber Pustekuchen! Nix is'. Was also tun? Was wir jetzt tun, wird in der Literatur als "Backtracking" bezeichnet. Wenn die Suche nicht mehr weiterkommt, erinnert sie sich schwach daran, dass in ihrem Container ja noch Knoten liegen, die sie anfangs als nich' so dolle abgestempelt hat. Tja - hinterher ist man immer klüger, geht auch Suchverfahren hin und wieder so. Also geht die Suche oben weiter und läuft dann sicher zum Ziel:  bzw. das eigentliche Beispiel mit der '3'. Der hier gefundene Weg ist nicht der Kürzeste, aber immerhin schon mal kürzer als der von der Tiefensuche vorgeschlagene Weg:  Wir sehen im unteren Teil der '3' einen Bereich, der leicht rot markiert ist. Das sind die Felder, für die sich das Suchverfahren interessiert hatte, weil sie dichter an Ziel lagen. Im Endeffekt hätten diese Felder aber nicht weitergeführt und gehören damit nicht zur endgültigen Wegstrecke. Diese Erkenntnis wurde aber vergleichsweise schnell gewonnen, wie wir an der Intensität des Rot-Tons feststellen können. (Wir erinnern uns: Je öfter ein Knoten vom Verfahren betrachtet wird, desto röter ...öhm... intensiver wird er rot gefärbt.) Nun ist es aber so, dass der gefundene Weg schon nicht schlecht ist, aber es geht noch kürzer. Klar ist das so, denn das Hillclimbing-Verfahren hat auch nie behauptet, den absolut kürzesten Weg finden zu können. Es gibt auch genug Szenarien, in denen das Hillclimbing-Verfahren von einer Sackgasse in die Nächste läuft und dadurch sehr ineffizient wird. Sicher ist nur: Wenn es eine Lösung gibt, so wird Hillclimbing mit Backtracking dieses auch finden - koste es, was es wolle, möchte man fast anfügen. Man kann Hillclimbing auch ohne Backtracking implementieren. Man sucht sich dann aus den Nachbarfeldern das aus, das am vielversprechendsten ist und verwirft die anderen. Geht auch - unter Umständen ist man dann in Sackgassen aber in den Allerwertesten gekniffen. Bleiben wir noch kurz bei der Wegstrecke. "Geht es noch kürzer?" ist die aktuelle Frage. Die Antwort lautet: "Ja, lassen wir doch mal A* ran". Die A*-Suche Wenn es eine Lösung gibt, dann findet die A*-Suche sie. Wenn es mehrere Lösungen gibt, dann findet die A*-Suche die "Beste" davon. Wir müssen der A*-Suche nur sagen, was "gut" ist. Klingt gut, oder? Allerdings hat sie Sache einen Haken: A* kostet deutlich mehr an Rechenkapazität als das, was wir bisher kannten. Bleiben wir dabei, dass wir die kürzeste Wegstrecke finden wollen. Auch A* betrachtet alle begehbaren Nachbarfelder und bewertet diese. Allerdings wird hier nicht wie beim Hillclimbing allein die verbleibende Wegstrecke als Maß der Dinge genommen, sondern zusätzlich auch die bisher angefallene Wegstrecke. Und genau das bringt den entscheidenden Vorteil. Bewertungskriterium ist die Summe aus dem Weg, der bereits gegangen worden ist und dem Weg, der noch zu gehen sein wird. Es wird ersichtlich, dass die A*-Suche tatsächlich alle Informationen beisammen hat, um die absolut kürzeste Strecke zu finden: 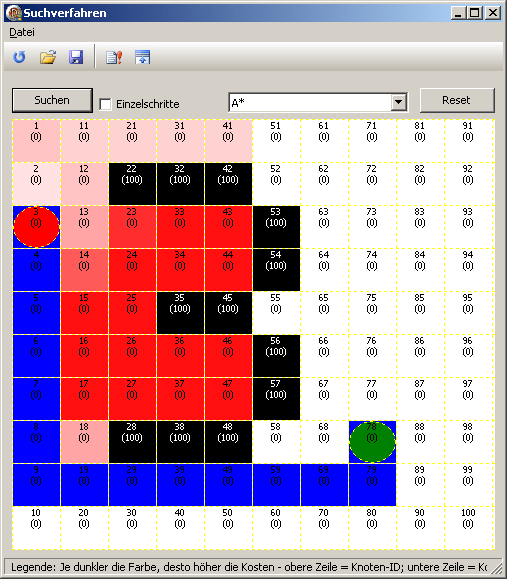 "Na bitte, warum denn nicht gleich so?" mag man fragen. Die Antwort liefert die Rotfärbung vieler Felder im Labyrinth. Zu nachweislich optimalen Ergebnissen zu kommen, kostet richtig Rechenzeit - und diese Zeit hat man nicht immer. Insgesamt waren 910 Schritte nötig, um zu diesem Ergebnis zu kommen. Das sind fast 35mal mehr Schritte als bei der Tiefensuche und immerhin noch 26mal mehr Schritte als beim Hillclimbing. Dafür aber auch garantiert optimal. Es lässt sich formal beweisen, dass die A*-Suche optimale Ergebnisse liefert, wenn sie korrekt bis zum Ende durchläuft. Ich verweise hier auf einschlägige Fachliteratur. Man kann mit A* aber noch etwas mehr Freude haben. Denken wir an ein Labyrinth, in dem es nicht nur Flächen und Mauern gibt, sondern auch Hügel. Und da wir quasi per se faul sind, wollen wir Hügel meiden und möchten einen Weg zum Ziel haben, der möglichst wenig hügelig ist - auch wenn er dafür eine Idee länger sein mag. Sehen wir uns folgendes Labyrinth an - je dunkler die Flächen sind, desto hügeliger sind sie auch, desto höher sind ihre Kosten.  Tja ... was ist jetzt der "optimale" Weg? Einer, der "nicht zu lang" und "nicht zu hügelig" ist. Was das konkret heißt, legen wir dirch eine angepasste Vergleichsfunktion selber fest, indem wir die Höhen und Strecken so gewichten, wie wir das eben möchten. Damit könnten wir entweder festlegen, dass die Höhen egal sind, weil wir sportlich sind und nur schnell auf kurzer Strecke zum Ziel wollen oder aber dass wir lieber eine Ewigkeit laufen, als mal den Berg hoch zu müssen. Und das können wir alles steuern, ohne den Algorithmus zu verändern - alleine die Vergleichsfunktion entscheidet. Das Ergebnis könnte wie folgt aussehen:  Die Technik und etwaige Fallstricke Unsere Suchverfahren sollen den Weg vom Start zum Ziel finden und gehen dabei allesamt in gleicher Art und Weise vor. Man setzt sie auf den Startpunkt und dann prüfen sie, wo sie denn so hin könnten. In unserem Fall sind das erstmal vier Felder, wenn kein Rand und keine Mauer im Weg ist: Bildlich gesprochen "links", "rechts", "oben" und "unten". Wir wählen also Nachbarfelder aus und bewerten diese (Hillclimbing, A*) oder lassen die Bewertung meinetwegen auch bleiben (Tiefensuche). Schön und gut. Eine Vergleichsfunktion liefern wir selbst und können somit bestimmt, nach welchen Kriterien bewertet werden soll. Die Vergleichsfunktion bestimmt also, in welcher Reihenfolge die Felder in unserem Containe landen und damit, in welcher Richtung wir als nächstes weiterlaufen werden. Denn eines ist bei allen Verfahren auch immer konstant: Wir gehen als nächstes auf das Feld, das im Container "oben" ist. Zyklenerkennung oder "Hilfe, ich laufe im Kreis und mir wird schlecht" Diese Nachbarfelder stellen also Kandidaten für unseren nächsten Schritt durch das Labyrinth dar. Aber eine Sache darf uns keinesfalls passieren: Dass wir im Kreis laufen. Wir dürfen also nicht wieder auf ein Feld kommen, auf dem wir bereits waren. "Hach - dann hau' ich die benutzten Felder doch in eine Liste" könnte ein erster Ansatz sein. Leider kommt man damit nicht weit. Wie wir gesehen haben, schauen sich die Algorithmen einzelne Felder durchaus häufiger an und kommen dabei vielleicht sogar aus verschiedenen Richtungen. Es geht also gar nicht um die Felder, die wir uns irgendwann schon mal angesehen haben, sondern um die Felder auf denen wir tatsächlich bisher längs gelaufen sind. "Hach, dann hau' ich die doch in eine Liste" könnte der Ansatz sein. Nein - wieder falsch. Denken wir an das Backtracking: Wir laufen vielleicht erst in die eine, dann in die andere Richtung - müssen also ggf. mehrere Wege im Hintergrund vorhalten. Mehrere voneinander unabhängige Wege, die unter Umständen ein und dasselbe Feld beinhalten können. Die Lösung ist ganz simpel und wird durch eine einfach verkettete Liste realisiert. Von meinem aktuellen Standpunkt aus gehe ich so lange ein Feld zurück, bis ich beim Start bin oder feststelle, dass ich über eines der mir angebotenen Nachbarfelder laufe. Wenn das der Fall ist, muss ich dieses Nachbarfeld auf jeden Fall verwerfen, weil ich sonst in einem Kreis laufe. (Wir erinnern uns: Algorithmen, die im Kreise laufen, haben es oftmals mit dem Terminieren etwas schwer...) Allgemeine Algorithmen vs. spezielle "Nodes" Schön an dieser Lösung ist die Tatsache, dass die gesamte Logik in den Feldern ("Nodes") des Labyrinths liegt. Nur sie müssen wissen, was sie kosten und in welcher Richtung es weitergeht. Der Such-Algorithmus hat keine Ahnung davon. Das ist wirklich ...sexy... und führt dazu, dass wir die Problemstellung beliebig austauschen können, ohne den Algorithmus zu ändern. Der Algorithmus braucht lediglich die Felder ("Nodes") sowie Vergleichsoperation. Fertig. Jetzt sind wir auch an dem Punkt angelangt, an dem ersichtlich wird, warum diese Verfahren allesamt fast identisch sind. Sie unterscheiden sich nur in der Vergleichsfunktion. Der Rest bleibt gleich. Das wiederhole ich doch gleich mal, weil es wichtig ist: Der Rest bleibt gleich. Ich kann mir von diesem Algorithmus auch eine Zugverbindung von Hamburg nach München raussuchen lassen, wenn ich die nötigen Informationen in die Nodes ("mögliche Zugverbindungen") stecke. Diese Trennung von Algorithmus und durchsuchtem Szenario zu schaffen, war eigentlicher Inhalt der Aufgabe, mit der wir uns in der Uni beschäftigt haben. Der Code im Anhang ist mitten im Semester entstanden und soll lediglich dazu dienen, diese verschiedenen Ergebnisse mit ihren Eigenschaften zu demonstrieren und dieser Aufgabe wird er sehr gerecht. Ich fand es zu schade, diesen Code in der Schublade verschwinden zu lassen und darum habe ich diesen Artikel drum herum geschrieben. Das Programm ist simpel und auch wenn ich es mit Delphi 2006 erstellt habe, sollten frühere Delphi-Versionen keine größeren Schwierigkeiten damit haben. Wer mag, kann auch nur die EXE-Datei starten und dann ein Labyrinth seiner Wahl laden.
Daniel R. Wolf
mit Grüßen aus Hamburg |
|
|
| Ansicht |
 Zur Linear-Darstellung wechseln Zur Linear-Darstellung wechseln |
 Zur Hybrid-Darstellung wechseln Zur Hybrid-Darstellung wechseln |
 Baum-Darstellung Baum-Darstellung |
ForumregelnEs ist dir nicht erlaubt, neue Themen zu verfassen.
Es ist dir nicht erlaubt, auf Beiträge zu antworten.
Es ist dir nicht erlaubt, Anhänge hochzuladen.
Es ist dir nicht erlaubt, deine Beiträge zu bearbeiten.
BB-Code ist an.
Smileys sind an.
[IMG] Code ist an.
HTML-Code ist aus. Trackbacks are an
Pingbacks are an
Refbacks are aus
|
|

| Erstellt von | For | Type | Datum |
| A* (A-Stern) - Algorithmus | This thread | Refback | 24. Mär 2011 07:32 |
| C-Sharp-Forum.de - Pathfind | This thread | Refback | 28. Nov 2010 12:42 |
| Delphi-Forum.de - Pathfind | This thread | Refback | 28. Nov 2010 02:10 |
| Nützliche Links |
| Heutige Beiträge |
| Sitemap |
| Suchen |
| Code-Library |
| Wer ist online |
| Alle Foren als gelesen markieren |
| Gehe zu... |
| LinkBack |
 LinkBack URL LinkBack URL |
 About LinkBacks About LinkBacks |
 Daniel
Daniel